Daftar Isi
Halo, Sahabat Gurulesprivate!
Apa itu barisan geometri? Apakah kalian pernah mendengarnya?
Dalam aritmetika, barisan geometri adalah serangkaian bilangan yang setiap angka berikutnya diperoleh dengan mengalikan angka sebelumnya dengan suatu rasio tetap.
Konsep ini memiliki aplikasi luas dalam matematika dan ilmu terkait. Nah, dalam artikel penjelasan kali ini, kita akan menjelajahi lebih dalam tentang materi satu ini, termasuk definisi, konsep, sifat-sifat, dan contoh penggunaannya.
Jadi, perhatikan baik-baik sampai habis ya!
Definisi Barisan Geometri

Sumber: Freepik
Barisan geometri adalah barisan bilangan yang setiap suku berikutnya diperoleh dengan mengalikan suku sebelumnya dengan suatu bilangan tetap yang disebut rasio atau faktor pengali.
Rasio ini biasanya dinotasikan sebagai ( r ). Dengan demikian, suku ke-( n ) dalam barisan geometri dapat dinyatakan sebagai:

Sampai di sini masih paham ya? Kita lanjut ke sifat-sifatnya!
Sifat-sifat Barisan Geometri
Adapun beberapa sifat yang penting kalian pahami mengenai materi ini, antara lain:
Baca juga: TEKS PROSEDUR BAHASA INGGRIS: PENGERTIAN, STRUKTUR, CARA MEMBUAT, DAN CONTOH
1. Rasio atau Faktor Pengali
Setiap suku dalam barisan diperoleh dengan mengalikan suku sebelumnya dengan suatu rasio tetap.
2. Perbandingan Antara Suku
Perbandingan antara suku-suku berturut-turut dalam barisan geometri adalah konstan.
3. Rumus Umum
Ada rumus umum untuk menentukan suku ke-n, yaitu sebagai berikut:

4. Jumlah Suku
Adapun jumlah suku ( n ) suku pertama dalam barisan geometri dapat dihitung dengan rumus berikut ini:

di mana ( Sn ) adalah jumlah suku dan ( n ) adalah jumlah suku yang dijumlahkan.
5. Unsur Terkecil dan Terbesar
Geometri dapat memiliki unsur terkecil dan terbesar, tergantung pada nilai rasio. Jika ( r > 1 ), maka barisan tersebut akan meningkat tanpa batas, dan jika ( 0 < r < 1 ), maka barisan akan mendekati nol.
Baca juga: Bimbel UTBK
Rumus-rumus Barisan Geometri

Sumber: Freepik
Rumus-rumus penting dalam materi satu ini yang harus kalian ketahui meliputi:
Baca juga: BENDA CAIR: PENGERTIAN, CONTOH SOAL DAN PEMBAHASAN | FISIKA KELAS 7 SMP

1. Rumus Umum Suku ke-n
Rumus umum untuk menentukan suku ke-n dalam barisan geometri adalah:

2. Jumlah (n) Suku Pertama ((Sn))
Rumus untuk menghitung jumlah (n) suku pertama dalam barisan geometri adalah:

di mana:
– (Sn) adalah jumlah total dari (n) suku pertama,
– (a1) adalah suku pertama dalam barisan,
– (r) adalah rasio atau faktor pengali, dan
– (n) adalah jumlah suku yang dijumlahkan.
3. Suku ke-n ((an)) dengan Jumlah (n) Suku Pertama ((Sn))
Rumus untuk menentukan suku ke-n dalam barisan geometri jika diketahui jumlah (n) suku pertama adalah:
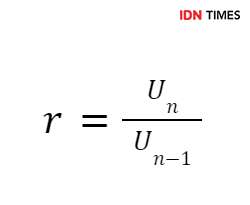
4. Jumlah Tak Hingga
Jika barisan geometri tidak memiliki batas atas, maka jumlah tak hingga (S{infty}) dapat dihitung menggunakan rumus berikut di bawah ini:

di mana (S{infty}) adalah jumlah tak hingga dari barisan geometri.
Baca juga : Bimbel SBMPTN
5. Unsur Terkecil dan Terbesar
Unsur terkecil ((a{min}})) dan terbesar ((a{{max}})) dalam barisan geometri dapat ditentukan berdasarkan nilai rasio ((r)):
– Jika (0 < r < 1), maka (a{{min}} = 0) dan (a{{max}} —> infty).
– Jika (r > 1), maka (a{{min}} —> 0) dan (a{{max}} —> infty).
Dengan menggunakan rumus-rumus di atas, kalian dapat melakukan berbagai perhitungan terkait dengan materi ini, seperti menentukan suku ke-n, menghitung jumlah suku, atau memprediksi perilaku barisan dalam jangka panjang.
Contoh Penggunaan Barisan Geometri

Sumber: Freepik
Materi satu ini memiliki banyak aplikasi dalam matematika dan ilmu terkait. Beberapa contoh penggunaannya meliputi:
1. Keuangan: Dalam keuangan, barisan geometri digunakan untuk menghitung pertumbuhan investasi atau hutang dengan suku bunga tetap.
2. Ilmu Fisika: Dalam ilmu fisika, materi ini dapat digunakan untuk memodelkan pertumbuhan populasi atau proses alami lainnya.
3. Teknologi: Dalam bidang teknologi, barisan geometri dapat digunakan untuk memodelkan pertumbuhan penggunaan data atau perangkat teknologi lainnya seiring waktu.
Sebagai konsep matematika penting yang memiliki banyak aplikasi dalam berbagai bidang, materi ini bukan hanya yang berkaitan dengan pendidikan, tetapi juga teknologi hingga sistem pembayaran.
Dengan pemahaman yang baik tentang definisi materi ini, sifat-sifat, dan contoh penggunaannya, kita dapat menggunakan barisan geometri secara efektif dalam pemecahan masalah dan analisis.
Contoh Soal dan Pembahasannya

Sumber: Freepik
Berikut ini beberapa contoh soal beserta pembahasannya mengenai barisan geometri agar kalian lebih mudah memahaminya:
Contoh Soal 1
Tentukan suku ke-5 dari barisan geometri berikut: 2, 6, 18, 54, …
Pembahasan 1:
Diketahui suku pertama ((a1)) = 2 dan rasio ((r)) = 3.
[an = a1 x r^{(n-1)}]
[a5 = 2 x 3^{(5-1)}]
[a5 = 2 x 3^4]
[a5 = 2 x 81]
[a5 = 162]
Jadi, suku ke-5 dari barisan geometri tersebut adalah 162.
Contoh Soal 2
Hitunglah jumlah 6 suku pertama dari barisan geometri dengan suku pertama 3 dan rasio 4.
Pembahasan 2:
Diketahui suku pertama ((a1)) = 3, rasio ((r)) = 4, dan jumlah suku ((n)) = 6.
[Sn = {{a1 x (r^n – 1)}} / {{r – 1}}]
[S6 = {{3 x (4^6 – 1)}} / {{4 – 1}}]
[S6 = {{3 x (4096 – 1)}} / {3}]
[S6 = {{3 x 4095}} / {3}]
[S6 = 4095]
Jadi, jumlah 6 suku pertama dari barisan geometri tersebut adalah 4095.
Contoh Soal 3
Tentukan suku ke-8 dari barisan geometri berikut: 5, -10, 20, -40, …
Pembahasan 3:
Diketahui suku pertama ((a1)) = 5, dan rasio ((r)) = -2
[an = a1 x r^{(n-1)}]
[a8 = 5 x (-2)^{(8-1)}]
[a8 = 5 x (-2)^7]
[a8 = 5 x (-128)]
[a8 = -640]
Jadi, suku ke-8 dari barisan geometri tersebut adalah -640.
Contoh Soal 4
Jika jumlah tak hingga ((S{infty})) dari suatu barisan geometri adalah 80 dan suku pertamanya adalah 10, tentukan rasio ((r)) barisan tersebut!
Pembahasan 4:
Diketahui jumlah tak hingga ((S{infty})) = 80 dan suku pertama ((a1))
[S{infty} = {{a1}} / {{1 – r}}]
[80 = {{10}} / {{1 – r}}]
[80(1 – r) = 10]
[80 – 80r = 10]
[80r = 70]
[r = {{70}} / {{80}}]
[r = {{7}} / {{8}}]
Jadi, rasio ((r)) -nya adalah {{7}} / {{8}}
Contoh Soal 5
Hitunglah jumlah tak hingga (\(S_{\infty}\)) dari barisan geometri dengan suku pertama 2 dan rasio 0.5.
Pembahasan 5:
Diketahui suku pertama ((a1)) = 2 dan rasio ((r)) = 0.5
[S{infty} = {{a1}} / {{1 – r}}]
[S{infty} = {{2}} / {{1 – 0.5}}]
[S{infty} = {{2}} / {{0.5}}]
[S{infty} = 4]
Jadi, jumlah tak hingga ((S{infty})) tersebut adalah 4.
Contoh Soal 6
Diketahui sebuah barisan geometri memiliki suku pertama (a1 = 3) dan rasio (r = 2). Tentukan suku ke-4 dari barisan tersebut.
Pembahasan:
Rumus umum untuk suku ke-n adalah (an = a1 x r^{(n-1)}). Substitusi nilai (a1) dan (r) ke dalam rumus tersebut:
[a4 = 3 x 2^{(4-1)}]
[a4 = 3 x 2^3]
[a4 = 3 x 8]
[a4 = 24]
Jadi, suku ke-4 dari barisan tersebut adalah 24.
Contoh Soal 7
Sebuah barisan geometri memiliki suku pertama (a1 = 5) dan suku ke-5 (a5 = 80). Tentukan rasio dari barisan tersebut..
Pembahasan:
Kita dapat menggunakan rumus umum untuk suku ke-n untuk menemukan rasio (r):
[an = a1 x r^{(n-1)}]
Substitusi nilai (a1), (a5), dan (n) ke dalam rumus:
[80 = 5 x r^{(5-1)}]
[80 = 5 x r^4]
[r^4 = {80} / {5}]
[r^4 = 16]
[r = [4] akar {16]
[r = 2]
Jadi, rasio dari barisan tersebut adalah 2.
Contoh Soal 8
Sebuah barisan geometri memiliki jumlah suku pertama (S3 = 28) dan suku ke-5 (a5 = 32). Tentukan suku pertama dan rasio dari barisan tersebut..
Pembahasan:
Kita akan menggunakan rumus untuk jumlah (n) suku pertama untuk menentukan suku pertama (a1):
[Sn = {{a1 x (r^n – 1)}} / {{r – 1}}]
Substitusi nilai (S3) dan (n) ke dalam rumus:
[28 = {{a1 x (r^3 – 1)}} / {{r – 1}}]
Kita juga telah diberikan (a5 = 32), yang artinya (a5 = a1 x r^{(5-1)}). Kita bisa menggunakan informasi ini untuk mencari nilai (a1).
[32 = a1 x r^4]
[a1 = {{32}} / {{r^4}}]
Kemudian, kita bisa substitusi nilai (a1) yang baru ke dalam persamaan (S3).
[28 = {{{{32}} / {{r^4}} x (r^3 – 1)}} / {{r – 1}}]
Setelah itu, kita bisa selesaikan persamaan tersebut untuk mencari nilai (r). Setelah menemukan nilai (r), kita bisa kembali substitusi ke persamaan (a1) untuk mencari nilai (a1).
Contoh Soal 9
Diketahui sebuah barisan geometri memiliki suku pertama (a1 = -2) dan jumlah tak hingga (S{infty} = 8). Tentukan rasio dari barisan tersebut.
Pembahasan:
Rumus untuk jumlah tak hingga (S{infty}) adalah (S{infty} = {{a1}} / {{1 – r}})
Substitusi nilai (a1) dan (S{infty)) ke dalam rumus:
[8 = {{-2}} / {{1 – r}}]
[8(1 – r) = -2]
[8 – 8r = -2]
[8r = 10]
[r = {{10}} / {8}]
[r = {{5}} / {4}]
Jadi, rasio dari barisan tersebut adalah ({{5}} / {4})
Contoh Soal 10
Sebuah barisan geometri memiliki suku pertama (a1 = 125) dan suku ke-4 (a4 = 5). Tentukan jumlah (n) suku pertama barisan tersebut.
Pembahasan:
Kita dapat menggunakan rumus umum untuk suku ke-n untuk menentukan rasio (r).
[a4 = a1 x r^{(4-1)}]
Substitusi nilai (a1), (a4), dan (n) ke dalam rumus:
[5 = 125 x r^3]
[r^3 = {5} / {125}]
[r^3 = {1} / {25}]
[r = [3] akar {{1} / {25}}]
[r = {1} / {5}]
Kemudian, kita bisa menggunakan rumus untuk jumlah (n) suku pertama untuk menemukan nilai (n).
[Sn = {{a1 x (1 – r^n)}} / {{1 – r}}]
Substitusi nilai (a1) dan (r) ke dalam rumus:
[Sn = {{125 x (1 – ({1} / {5})^n)}} / {{1 – {1} / {5}}}]
[Sn = {{125 x (1 – {1} / {5})^n}} / {{4} / {5}}]
Dari sini, kita bisa lanjutkan perhitungan untuk mencari nilai (n).
Jika masih ada banyak pertanyaan yang perlu kalian tanyakan mengenai materi barisan geometri, konsultasikan segera bersama tim pengajar profesional kami.
Jadi, apa lagi yang ditunggu? Hubungi kami segera di line telepon (021) 77844897 atau kamu juga bisa menghubungi kami via 0877-8160-9961. Atau klik www.gurulesprivate.co.id untuk mendapatkan informasi lebih lanjut.
Sampai ketemu di Guru Les Private!
Referensi:
- detik.com
- katadata.co.id


