Daftar Isi
Halo sobat Gurulesprivate!
Saat mempelajari matematika di sekolah, mungkin kamu pernah belajar tentang identitas trigonometri. Materi ini merupakan salah satu cabang dalam ilmu matematika yang mempelajari sudut segitiga seperti sinus, cosinus, dan tangen. Bagi kamu yang masih penasaran dan ingin belajar kembali tentang identitas trigonometri, yuk langsung simak artikel di bawah ini untuk melihat penjelasan lengkapnya.
Identitas trigonometri adalah rumus atau persamaan yang melibatkan fungsi trigonometri dan berlaku untuk semua sudut tertentu. Identitas ini sangat penting dalam matematika, terutama dalam pemecahan masalah yang melibatkan segitiga dan gelombang periodik.
Sejarah trigonometri mencerminkan perkembangan matematikawan dari berbagai budaya dan periode waktu, yang berkontribusi pada pemahaman kita tentang hubungan antar fungsi trigonometri. Berikut adalah garis besar perkembangan trigonometri dari masa ke masa.
Baca juga: Bimbel sbmptn
Sejarah Identitas Trigonometri

Sumber: Freepik
1. Zaman Kuno dan Awal
Mesopotamia dan Mesir Kuno: Meskipun konsep trigonometri formal belum ada, orang Mesopotamia dan Mesir sudah menggunakan konsep-konsep geometris yang terkait dengan sudut dan panjang sisi dalam konteks perhitungan astronomi dan arsitektur.
India Kuno: Matematikawan India kuno seperti Aryabhata (476–550 M) dan Bhaskara I (600–680 M) mulai mengembangkan tabel sinus dan kosinus serta trigonometri dasar. Aryabhata adalah salah satu orang pertama yang memperkenalkan konsep sinus dalam bentuk tabel.
2. Sepatu Abad
Islam dan Dunia Arab: Pada abad ke-8 hingga ke-11, matematikawan Islam seperti Al-Khwarizmi, Al-Battani, dan Omar Khayyam memperluas dan memperdalam teori trigonometri. Al-Battani (858–929 M) membuat tabel sinus yang sangat akurat dan memformalkan identitas trigonometri dasar. Khayyam juga mengkaji dan mengembangkan teori trigonometri dalam konteks astronomi.
3. Abad ke-16 hingga ke-17
Renaissance Eropa: Pada periode ini, trigonometri menjadi lebih sistematis dengan adanya perkembangan dalam notasi dan teori. Regiomontanus (1436–1476) dan Johannes Kepler (1571–1630) membuat kemajuan besar dalam tabel trigonometri dan identitas. Regiomontanus mengkaji trigonometri dasar, sedangkan Kepler memanfaatkan trigonometri dalam studi astronomi.
Leonhard Euler: Pada abad ke-18, Leonhard Euler (1707–1783) memperkenalkan banyak trigonometri yang masih digunakan hingga sekarang. Euler mengembangkan dan menggeneralisis identitas trigonometri serta memperkenalkan notasi yang lebih formal.
4. Abad ke-19
Abstrak Matematika dan Teori: Pada abad ke-19, perkembangan lebih lanjut dalam teori trigonometri dilakukan oleh matematikawan seperti Augustin-Louis Cauchy dan Joseph Fourier. Teori Fourier mengembangkan deret Fourier, yang menggunakan trigonometri untuk menyatakan fungsi periodik sebagai jumlah deret sinus dan kosinus.
5. Abad ke-20 dan ke-21
Penerapan Modern: Dengan perkembangan komputasi dan analisis numerik, trigonometri digunakan dalam berbagai bidang, termasuk fisika, teknik, dan ilmu komputer. Identitas ini membantu dalam penyelesaian masalah yang melibatkan gelombang, osilasi, dan sinyal.
Pengembangan Komputasi dan Aplikasi: Di era digital, trigonometri digunakan dalam pemrograman komputer, grafika komputer, dan analisis data. Algoritma dan perangkat lunak modern memanfaatkan identitas ini untuk perhitungan numerik dan visualisasi.
Baca juga: bimbel utbk
Manfaat Mempelajari Identitas Trigonometri
Berikut adalah manfaat dari mempelajari trigonometri dan bagaimana konsep ini dapat diaplikasikan dalam berbagai konteks:
1. Meningkatkan Pemahaman Matematika Dasar
Trigonometri merupakan bagian integral dari matematika dasar. Dengan memahami trigonometri, siswa dapat meningkatkan keterampilan matematika mereka secara keseluruhan. Konsep ini membantu siswa memahami hubungan antara sudut dan panjang sisi dalam segitiga, yang merupakan dasar dari banyak topik matematika lainnya.
2. Aplikasi dalam Sains dan Teknik
Trigonometri sering digunakan dalam berbagai bidang sains dan teknik. Misalnya, dalam fisika, trigonometri digunakan untuk memecahkan masalah yang melibatkan gelombang, getaran, dan medan listrik. Dalam teknik, trigonometri membantu merancang merancang struktur, menganalisis sistem mekanik, dan memodelkan fenomena fisik.
3. Menyederhanakan Persamaan Matematika
Salah satu manfaat utama dari mempelajari trigonometri adalah kemampuan untuk mencapai persamaan matematika yang kompleks. Dengan menggunakan trigonometri, siswa dapat mengubah dan memanipulasi persamaan untuk membuatnya lebih mudah diselesaikan. Ini sangat berguna dalam menyelesaikan masalah matematika lanjutan.
4. Meningkatkan Kemampuan Pemecahan Masalah
Pemahaman yang baik tentang trigonometri membantu meningkatkan kemampuan pemecahan masalah siswa. Identitas ini memberikan alat dan teknik yang diperlukan untuk memecahkan berbagai masalah, baik dalam matematika murni maupun terapan. Kemampuan ini sangat berharga dalam banyak bidang profesional.
Baca juga: Les privat
Dasar-dasar Trigonometri

Sumber: Freepik
Sebelum masuk ke identitas trigonometri, penting untuk memahami fungsi trigonometri dasar:

Di mana “depan” adalah panjang sisi yang berseberangan dengan sudut θ , “sebelah” adalah panjang sisi yang bersebelahan dengan sudut θ , dan “miring” adalah panjang sisi miring dari segitiga siku-siku.
Identitas Trigonometri Dasar
Berikut adalah beberapa dasar trigonometri yang sangat penting:
1. Identitas Pythagoras
Identitas Pythagoras adalah salah satu trigonometri yang paling mendasar. Ini berasal dari Teorema Pythagoras dalam segitiga siku-siku:
![]()
Dengan identitas ini, kita dapat menemukan nilai satu fungsi trigonometri jika kita mengetahui nilai fungsi trigonometri yang lain.
2. Identitas Kebalikan
Identitas kebalikannya adalah hubungan antara fungsi trigonometri dan kebalikannya:
![]()
3. Identitas Tangen
Identitas tangen adalah hubungan antara tangen dan fungsi sinus dan kosinus:
![]()
4. Identitas Sudut Ganda
Identitas sudut ganda melibatkan fungsi trigonometri dari sudut yang dua kali lipat:
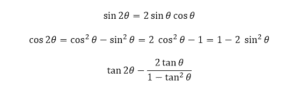
5. Identitas Sudut Setengah
Identitas sudut menghubungkan setengah fungsi trigonometri dari sudut yang setengah kali lipat:

Baca juga: Les privat jakarta
Rumus Identitas Trigonometri

Sumber: Freepik
Usai mengerti tentang trigonometri serta petunjuknya, berikut ini rumus-rumus identitas trigonometri yang harus kamu ketahui:
(dosa α)(dosa α) + (cos α)(cos α) = 1
(tan α)(tan α) + 1 = (detik α)(detik α)
(tempat tidur α)(tempat tidur α) + 1 = (csc α)(csc α)
dosa(90 − α)° = cos α°
cos(90 − α)° = sin α°
tan(90 − α)° = cot α°
cot(90 − α)° = tan α°
detik(90 − α)° = csc α°
csc(90 − α)° = detik α°
cos(180 − α)° = −cos α°
tan(180 − α)° = −tan α°
tempat tidur(180 − α)° = −tempat tidur α°
detik(180 − α)° = −detik α°
csc(180 − α)° = csc α°
dosa(180 + α)° = −sin α°
cos(180 + α)° = −cos α°
tan(180 + α)° = tan α°
sin(360 − α)° = sin (−α°) = −sin α°
cos(360 −α)° = cos (−α°)= cos α°
tan(360 −α)° = tan (−α°) = − tan α°
sin(α + n.360)° = sin α°
cos(α + n.360)° = cos α°
tan(α + n.180)° = tan α°
Aplikasi Identitas Trigonometri

Sumber: Freepik
Trigonometri digunakan dalam berbagai aplikasi, termasuk matematika, fisika, teknik, dan bahkan seni. Berikut beberapa contoh penerapannya:
1. Memecahkan Persamaan Trigonometri
Trigonometri sering digunakan untuk memecahkan dan memecahkan persamaan trigonometri. Misalnya, jika kita memiliki persamaan sin 2 x + cos 2 x =1, kita dapat menggunakan identitas Pythagoras untuk menyelesaikannya.
2. Analisis Gelombang
Dalam fisika, trigonometri digunakan untuk menganalisis gelombang, seperti gelombang suara dan gelombang cahaya. Fungsi sinus dan kosinus digunakan untuk menggambarkan gelombang sinusoidal, yang merupakan dasar dari banyak fenomena fisik.
3. Teknik Elektronika
Dalam teknik elektronika, identitas trigonometri digunakan untuk menganalisis sinyal dan sistem. Misalnya, dalam analisis Fourier, sinyal dipisahkan menjadi komponen-komponen sinusoidal, yang kemudian dianalisis menggunakan identitas trigonometri.
4. Desain Grafis
Dalam desain grafis dan animasi komputer, identitas trigonometri digunakan untuk menciptakan rotasi, skala, dan transformasi objek. Fungsi trigonometri digunakan untuk menghitung posisi, rotasi, dan skala objek dalam ruang tiga dimensi.
Jadi, apa lagi yang ditunggu? Hubungi kami segera di saluran telepon (021) 77844897 atau Anda juga dapat menghubungi kami melalui 085810779967 . Atau klik www.gurulesprivate.co.id untuk mendapatkan informasi lebih lanjut.
referensi:
- kumparan.com
- detik.com


